Tag Archives: sbg

Memories from MAAthfest 2018

Posted on by
2

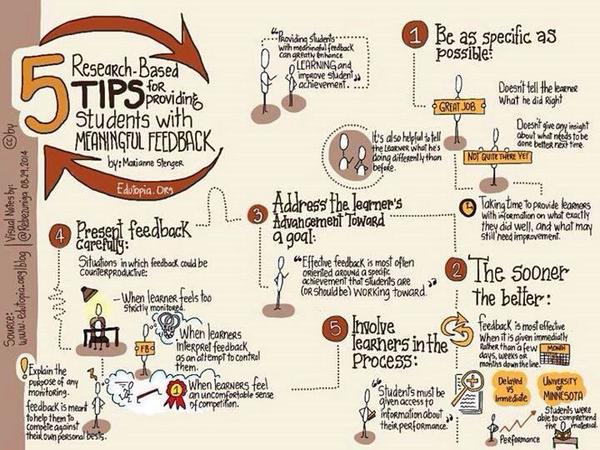
0. At #MAAthfest this past August, Drew Lewis asked, “How can we make sure we are providing adequate opportunities for all our students to demonstrate mastery?“

This year’s MAAthfest was held in Denver, Colorado from August 1st through August 4th. I went, I had a great time, and I want to tell you about some of the things I learned. While there, I presented twice: once as an invited panelist for Project NExT and then as a speaker in the Special Session on #MasteryGrading. Info about my talks is available here in my blog post called “MAAthfest 2018“.

Now I hope to give you a quick summary of some of the many great take-aways from the rest of the #MasteryGrading session.

1. Many of us noted that Mastery Grading reduces stress levels, both for the instructors and the students.

2. It’s hard to get by on a partial credit strategy. Mastery Grading holds students accountable for their own learning.

3. Many of us moved toward Mastery Grading after spending a long time really considering questions like “Why do we assign grades?” and “What do we want grades to tell us?”

4. I really like, respect, and enjoy these people.

We didn’t spend the entire time working. We also had shared some great meals:

5. Traditional Grading expects all students to learn material at the same pace, but Mastery Grading allows learners to find their own path.

6. Mastery Grading really changes the way you write questions. If your goal is for students to change how they answer questions, sometimes you have to change what you’re asking them.

7. In Traditional Grading, instructors give students points. In Mastery Grading, students have accountability for gaining and then displaying knowledge.

8. There are many different ways to implement Mastery Grading. The real challenge is  finding the one that works best for you, your courses, and your students.

I’m excited to read an upcoming issue of PRIMUS (Problems, Resources, and Issues in Mathematics Undergraduate Studies) devoted to Mastery Grading. Submissions are due October 15th, 2018 and more information is available here.

9. In all learning, there’s struggle. Mastery Grading supports and encourages students through the struggle.

Austin added, “Assessment should guide students toward productive struggle” and I really like this quote. On Deadlines, he also gave us two pieces of important advice:

 

10. Mastery Grading allows a path for improvement and success for all students, while still keeping clear, high expectations for learning.

 

Bevin Maultsby (NC State) shared with us course grade distributions for students in a course on Matlab, a computer programming language. Over 60% of her students earned As! So impressive.

11. Some adaptations of Mastery Grading work well in project-based courses, courses with proofs, etc.

Chad Wiley (Emporia State University) told us about his use of specifications grading, and I’m hoping to adapt some specs-style setup in my upcoming “Math for Teachers” course that starts in October.

If you’re wondering about the difference between standards-based grading and specifications-based grading, Joshua Bowman (Pepperdine University) really summed it up well:

12. Common benefits of Mastery Grading include sustained student effort, clearer learning objectives, and changes in conversations with students.

We had a great three-presenter talk about #SBG happening at three different institutions:

I really need to look back on this list of “14 Characteristics for Evaluating Grading Systems” by Linda Nilson.

13. The Mastery Grading community has begun gathering powerful data about student learning, and we’re seeing that Mastery Grading allows for students to be successful even with differentiated pacing of their learning.

Drew Lewis (South Alabama) had a really amazing slide called “A tale of two students” and I am committed to generating such graphs for my own students this semester:

Honestly, if I had to pick one slide that has stuck with me daily since MAAthfest, it’s Drew’s graph of the learning trajectories of two different students. If we want all our students to have the opportunity to be successful, we must construct our courses that allows for differentiated learning trajectories. 

14. Most University grade systems are already built with Mastery vocabulary in their grading scales.

15. Occasionally I missed Tweeting great stuff.

There are several other talks I don’t have archived on Twitter. Joshua Bowman gave a great talk about his years of experience using standards-based grading. His work was what originally inspired me to make the Mastery Grading jump in my own courses in 2013-2014.

Steven Clontz gave some really great practical tips (and I was too busy taking notes to tweet them!). Thankfully, he did that part himself:

I wasn’t able to attend David Clark’s (from GVSU) presentation when he won the Alder Award, but here’s what the MAA tweeted:

16. Outside of Mastery Grading, I was inspired and found joy in several other places.

 Her slides are available here, courtesy of the MAA.

  • I went to Emily Riehl’s talk in the “Category Theory for All” session and her talk was amazing.


    I mentioned to a colleague here what I had learned about category theory and it turns out one of our graduate students at the College of Charleston is writing a masters thesis in this area. I was invited to join his thesis committee, so now I’m going to have the opportunity to learn a lot more. Emily’s talk reminded me of some of the things I love about universal algebra.

  • One of my best friends from childhood was able to fly to Denver to spend some time with me, and her company was the best gift. Also, this was my first trip away from my three children — ever! — and by the time she got there, I was hug-starved. So great to have someone to offer a hug (and a hundred laughs) each day.

See you at MAAthfest 2019.

Standards-Based Grading in Fall 2018

Posted on by
Reply

An Overview of My Semester

This semester, I’ll be teaching three different courses:

  • Pre-Calculus Mathematics (MATH 111), a course designed to review algebra and trigonometry for students who plan to take our (scientific) calculus sequence;
  • College Algebra (MATH 101), a course designed to cover algebra and function basics for students who will continue on either to MATH 111 (pre-calculus with trigonometry) or MATH 105 (business calculus); and
  • “Applications of Mathematics Across the Curriculum with Technology” (SMFT 516), a graduate-level course designed for in-service science & math teachers who are working toward an interdisciplinary M.Ed.

Due to enrollment challenges, my schedule for courses shifted in late July, so I spent a while during the summer trying to ditch my old plans for the semester and start over. Although I was planning to attend Mathfest in Denver, CO and give a talk in the session on #MasteryGrading based on my years of experience implementing standards-based grading in my courses, I must admit that before my trip I had no plans to use SBG in any of my courses this semester.

But then… UGH!!! INSPIRATION FROM PEOPLE. AND TOO MANY GOOD IDEAS.

So I attended every talk in the #MasteryGrading session at Mathfest. And wow, I got a ton of great ideas from all of the talks [stay tuned for future blog post] and, on a personal level, I really enjoyed our conversations, meals, and hang-outs outside of the session itself. (Thanks, y’all!)

Unfortunately a couple of days into Mathfest I realized I just couldn’t go back to traditional grading, so I threw out all my traditional plans for the semester and committed to myself that I would implement SBG/SBSG/MasteryGrading in 100% of my courses this semester.

Did I mention that I got home from Mathfest only 15 days in advance of my semester start?

The Nuts and Bolts of Fall 2018: SBG PreCalculus and SBG College Algebra

Rachel Weir, of Allegheny College, is maintaining a repository of course documents for secondary Mathematics courses that are using Standards-based grading, Specifications-based grading, or Mastery-Based Grading: Rachel’s SBG Repository

Both my Pre-Calculus and College Algebra courses are using the exact same setup. It’s very similar to Tom Mahoney ‘s (@MathProfTom) approach in his College Algebra courses. Here is the basic setup:

  1. I have written 25 standards for each course.
  2. Every time a student completes a problem on a standard, I will assess the solution using a “SGN Rubric” (see below). This assigns either 0 points, 1 point, or 2 points to each attempt.
  3. A student’s score on a standard is the average of their best two attempts.
  4. A student earns total points out of 50 possible (25 standards*2 points max). Together with work in an online homework system, this converts to a usual letter grade*.

For example, for any given standard, I will track a student’s progress as something like “0,1,2,1,1,1,0,2” and this student will earn a 2. After two perfectly correct solutions, the student isn’t required to answer problems on that topic again.

*My department requires a departmental-wide final exam that is graded using a partial credit, percentage system, and this exam must be worth at least 25% of each student’s course grade. So the actual grade computation is (75% performance on standards)+(25% final exam performance).

Links to Possibly Useful Things

Here are some links that I’ve freely distributed to my students. Perhaps reading them will shine some light on how I explained this system to them. Also, there are more details about the “SGN Rubric” I mentioned above and explanation about online homework & how it fits in.

Things To Do Later

I haven’t mentioned that third class (“Applications of Mathematics Across the Curriculum with Technology”). It runs double speed for half the time, during our Express II semester, and it doesn’t start until October. I want this course to be a project-based course, so I’m going to figure out some way to introduce specifications grading into my design. Robert Talbert (@RobertTalbert) has written extensively about his use of specs-grading and it’s my plan to steal as many ideas from his MTH 350 F18 Syllabus as I can. Our courses are very different, but he has so many clever ideas for his course skeleton. Once I write my syllabus, I’ll tell you about it.

10 Minutes of Thoughts on My SBG Linear Algebra Class

Posted on by
4

I’ve been meaning to write a post about my standards-based Linear Algebra course for months, but the hectic schedule of the semester has kept me away from this task until now. Today was my last “content” day of Linear Algebra — we have two more classes remaining, one for a test day and another for a re-assessment day. This seemed like a good time for me to take ten minutes to gather some thoughts about how the semester went.

Standards List for Linear Algebra: https://www.overleaf.com/read/kycvnvzdvksw  (Availablle on Overleaf, which is awesome and I can’t recommend enough)

What Went Well: We ended up having 20 standards this semester. This is a little more than one per week (our semester has 16 instruction weeks). Overall, I think this was a good number of standards to have, and I’m happy with how they turned out. I tried to group them again by “Big Questions” to have a reference frame of what it is we’re trying to do in the course. Oddly, we tackled “Big Question 5” last (on inner product spaces), but I kept it numbered like that because of the textbook we are using. My basic idea was to come up with a Big Question for each chapter. For some stuff, this worked well (e.g., eigen-everything) but for other stuff we didn’t cover a whole lot (e.g., determinants).

I think I’m doing a better job of the sales-pitch aspect of a standards-based course. Many of my students expressed to me at various times that they really appreciated the ability to improve on past performance and that they were under less stress than in a traditional class. In a recent class meeting, a student wasn’t happy with the performance on the last quiz, and exclaimed, “Oh, thank goodness we have an exam on this soon!!!” [I asked the student for permission to share this quote.] I think this is one of the best things about my SBG courses — students really want to take an exam just to show what they know, whether that means showing mastery of current material, or showing mastery of material they struggled with earlier in the course.

My SBG approach definitely has some pros and also some cons, but the way it has shaped my interactions with students has always been a huge positive. Even with the sticky details that need to be cleaned up from this semester, I can’t imagine going back to a traditional grading scheme.

Room for Improvement: This semester was a little odd because we lost several days because of weather. Tropical Storm Hermine hit us, and we lost almost a week because of Hurricane Matthew. The re-shuffling of the academic calendar created a speed-bump that I never really recovered from. I hope next semester our calendar runs much more smoothly.

In particular, I am wondering about how I can improve in three areas. First, I want to expose my students to more applications of the material we are learning. I felt rushed all semester (related to shuffling of course calendar, maybe?) and so I didn’t ever feel like I had time to fit in cool applications, or videos on where people use this stuff “in the real world,” etc. A colleague teaching the same course required students to do group projects on applications of linear algebra & I believe the students presented them to the class at the end of the semester. This seems like a great idea, but I’m always nervous about assigning group projects because I remember how much I hated doing them as a student. It’s something I should consider more.

Second, all of my course standards are weighted equally. This has served me well in Calculus II and in other courses. But in Linear Algebra it became a little tricky, because part of what I was aiming to do was to have my students attempt to write proofs of mathematical statements. (The only mathematical background required for entry into my course is Calculus I, and that is for “mathematical maturity” as opposed to content reasons.) So some of my students were concurrently taking our “Introduction to Proofs” course, but others weren’t taking this course and won’t need it for their major. In general, my idea was to ask them to prove elementary results they had already seen in class. The problem I encountered is that a “write a proof” standard is really tough. How do I let them have multiple attempts? Is it okay if they end up never being able to prove stuff about, say, matrix inverses, but they can prove stuff about, say, subspaces of a vector space?

One idea I’ve had is to have the students keep a “Proof Portfolio” and grade it as either “complete” or “not” at the end of the semester. I’m sure there’s some specs-based approach I could implement for this, but I haven’t worked out what it would look like yet.

Third, trying to put together all my course materials on the fly is hard. All of the time, I was working on: Plans for class, writing exams, writing quiz questions, writing reassessment questions, putting together online homework, meeting with students for several hours a week outside of class, updating the list of standards regularly… I would admonish my summer-month self that I should do more of this “in my free time” before the term begins so I’m not under such a time crunch during the semester. But I am not great at this because I like building a course as it goes, as I see how the students are responding, as I see how the pace of the course unfolds, etc. Having to get all this done ahead of time would probably help me out a lot, but it’s tough to do. Thankfully some of my stuff from this semester can be re-used when I teach Linear Algebra next semester.

My ten minutes are done so I have to move on to the next task on my queue! I hope to add more later.

Standards-based Linear Algebra

Posted on by
2

This semester I’m teaching our introductory linear algebra course. As I did for Calculus II, I’ve implemented a standards-based assessment system. I’ve taken our course content and split it into “standards”, or little pieces of mathematics that I want my students to master. These standards are grouped together by what I call “Big Questions”. Here is what we’ve covered so far this semester:

  • Big Question #1: What are the tools for solving systems of linear equations?
    • 1.1: I can solve systems of linear equations using row operations. I can use Gaussian elimination with back-substitution to solve systems of linear equations. I can use Gauss-Jordan elimination to solve systems of linear equations.
    • 1.2: I can characterize the solutions to systems of linear equations using appropriate notation and vocabulary.
    • 1.3: I can use matrix inverses to solve systems of linear equations.
    • 1.4: I can find and use an LU-factorization of a matrix to solve a system of linear equations.
  • Big Question #2: What is the fundamental structure of the algebra of matrices?
    • 2.1: I can perform algebraic operations with matrices, including addition, subtraction, scalar multiplication, and matrix multiplication. I can compute the transpose of matrices.
    • 2.2: I can find the inverse of matrices using Gaussian elimination. I can find the inverse of matrices using a product of elementary matrices.
    • 2.3: I can demonstrate theoretical connections about properties in the algebra of matrices.
  • Big Question #3: How can we characterize invertible matrices?
    • 3.1: I can find determinants using cofactor expansion. I can find determinants using row or column operations.
    • 3.2: I can demonstrate theoretical connections between statements equivalent to “the matrix A is invertible.”
    • 3.3: I can demonstrate theoretical connections between matrix equations, vector equations, and systems of linear equations, and their properties and solutions.
  • Big Question #4: What are vector spaces & how can we describe them?
    • 4.1: I can prove whether an algebraic structure is a vector space (or not) using the vector space axioms. I can prove whether or not a subset W of a vector space V forms a subspace. I can determine and characterize subspaces of $\mathbb{R}^n$.
    • 4.2: I can write a proof showing whether a subset of vectors from a vector space forms a spanning set for the vector space (or not). I can write a proof to show whether a subset of vectors from a vector space is linearly independent (or not). I can determine whether a set of vectors forms a basis for a vector space. I can find the dimension of a vector space.
    • 4.3: I can find a basis for the row space, the column space, or the null space of a matrix. I can determine the rank and nullity of a matrix. Given a consistent system Ax=b, I can describe the general solution in the form x=xp+xh
    • 4.4: I can demonstrate knowledge of the theory of vector spaces by proving elementary results and theorems.

The remaining Big Questions are:

  • Big Question #5: What are inner product spaces and how can we describe them?
  • Big Question #6: What kinds of functions map one vector space into another while preserving vector space operations?
  • Big Question #7: What are eigenvalues and why are they useful?

Our first exam was last week, so today has been Re-Assessment Central in my office. I’ll hand back our exams tomorrow and I’m hoping to talk with my students more about standards-based grading and how they can improve their standing in the course.

An Adventure in Standards Based Algebra

Posted on by
2

This semester I am teaching several sections of “Math 101: College Algebra”. One section uses an “emporium” method, where students work independently in a computer lab. Instructors are available for questions and we also hold mini-lessons as needed, during which small groups of students can work on a particular topic at the same time. The other two sections are “traditional” in format and I’ve designed a standards-based grading system for them.

I began by creating a list of 30 standards for our 16-week semester. These are grouped by textbook section. Each standard has one or more “I can…” statements associated with it. Here’s the complete list. I’m giving three midterm tests this semester and each test will have an assortment of problems. The exam I gave this week covered our first six standards and had fourteen problems. Not all standards had the same number of problems.

I graded each problem using a modified “ERMF Rubric” (see http://www.nctm.org/Publications/mathematics-teacher/2004/Vol97/Issue1/EMRF_-Everyday-Rubric-Grading/). If you aren’t familiar with ERMF, I’d suggest checking out this post by Taylor Belcher, or some examples of the ERMF Rubric used in a beginning physics course. I decided I didn’t like the baggage associated with an “F” so I made mine an “ERMN” rubric:

ermn

Basically, I’m implementing a “Pass/Fail” system — although I refer to those as “Proficient” and “Not Proficient.” Scores of “E” and “M” are passing scores, and scores of “R” and “N” are failing scores. If a student earns all “E”s and “M”s on problems from a particular standard, then they get a “Proficient”. If there’s a mixture of some “R”s or “N”s, I looked at those case-by-case to determine if the student had shown enough understanding of the relevant ideas to merit a “Proficient” or not.

Overall, grading the exams took about one minute per exam page. I have about 50 students and this exam contained 6 pages. I don’t think this is too far off what it would have taken, time-wise, to grade using a traditional points- or percentage-based system.

I’m allowing students to come to my office for re-assessments, so any standards that earned a score “Not Proficient” can be improved upon later. In an upcoming post, I’ll write about my “Policy for Re-Assessments” and outline my system. From past experience, one key factor I’ve found is limiting the number of standards that can be re-attempted to no more than one per week.

At the end of the semester, 50% of the course grades will come from how they perform on their midterm tests. I’m converting all these “Proficients” and “Not Proficients” into a numeric score using this formula: “Midterm Exam Grade = 25 + 75*(# Proficient)/(# Total)”. Basically, this is the percentage of standards ranked Proficient, plus a tiny bit. Now I have to run off to class to return exams to students and explain more about how this grading system works — and why I believe it is to their advantage.

 

Documents related to SBG

Posted on by
3

This afternoon I’ll be presenting about standards based grading as part of Teaching, Learning and Technology‘s “Faculty Showcase.” I’ll be giving a similar talk at an upcoming conference. In case you’re interested, here are some documents related to my presentations:

A lot of my FAQ document was borrowed from Joshua Bowman (@Thalesdisciple). This semester, I didn’t actually give my students the FAQ document — It turned out that after three semesters of SBG, my explanation to students about how our grading system works & why I think it’s a good idea has gotten a lot better.

Actually, that point speaks to one of the great things I’ve gotten out of using SBG: Implementing my system forced me to give deep consideration to exactly what mathematical content I want my students to get out of the course. Instead of debating if homework should count 10% or 12% of the overall grade, or what I should do if a student misses a quiz for an undocumented reason, or other administrative policies like those, the SBG system made my entire course planning process focus on the math stuff I want to teach and assess — instead of worrying about policies unrelated to mathematics (compliance with the rules, attendance, percentage breakdowns, etc).

Two Upcoming Talks on Standards Based Grading

Posted on by
Reply

In the next month or so, I’ll be giving two talks on my implementation of standards based grading. (Okay, if you want to be really precise, that should say that I’m giving the same talk twice.) The first will be hosted by our “Teaching, Learning, and Technology” (@TLTCofC) division as part of their events for “Assessment Week”, and it will be on Wednesday, April 1st at 2pm. The second will be at SOCAMATYC  — the South Carolina Mathematical Association of Two-Year Colleges Annual Conference. They haven’t finalized their schedule yet, but the conference runs Friday 4/17 through Saturday 4/18. Thanks go to Frank Monterisi (@frank314) for letting me know about this opportunity.

Here’s a blurb about my talk:

In this presentation, we will give an overview of standards based grading (SBG) including helpful answers to questions of the form “What?”, “Why?” and “How?”. While an implementation specific to Calculus II will be discussed, the method outlined could be applied to courses in any discipline. If you’ve ever wondered about alternatives to traditional grading and how to avoid hearing the question, “What percent do I need to make on the final exam to get an 82% in the class?” then this is a great place to start.

Once I have put together my slides, I’m hoping to upload them here, along with some updated SBG documentation from my Calculus II course, like my current list of standards and the information provided to students about how the grading system works.

In a way, it feels a little strange to prepare a talk about standards based grading when I feel like the relative newbie to this topic. My entire system came about after many conversations and interactions with fellow educators on Twitter, and I am still indebted to them for all of their helpful support and guidance. In particular, I couldn’t have gotten my course running smoothly without inspiration from Frank Noschese (@fnoschese) and Joshua Bowman (@thalesdisciple). A quick google search just told me that Joshua gave a similar talk about his transition to SBG; I stumbled on his slides here.

Reflection on Standards-Based Calculus

Posted on by
Reply

Our semester is wrapping up and we only have one more class meeting day after Thanksgiving. I’ve been teaching two sections of “Calculus II” using my standards-based grading system that I’ve mentioned before. I think I made several improvements this semester and I wanted to share them, along with a couple of things I’m still contemplating. But first, here are things I thought went well:

  • I really liked having my standards organized by Big Questions. This is probably something I could have implemented outside of my grading system. Somehow writing and organizing my list of standards gave me the motivation and time and priority to think about the take-aways I wanted my students to get from our course.
  • Last Spring, I had approximately 18 standards, meaning about one per week. They were large learning targets. Take, for example, the “Techniques of Integration” standard that encompassed a couple of weeks of class time spent talking about integration by parts, by trigonometric identities, by trigonometric substitution, by partial fractions, and so on. This semester, I wanted more standards that were more specific. I hit my goal of 30 standards for the semester and this number worked well. On the one hand, the standards were specific enough that students could focus on just one idea at a time. On the other hand, there weren’t an unreasonable number for me to assess. Roughly they correlated to one standard per textbook section, spanning about 1.5 classes per idea.
  • Originally, I had a “policy of replacement” where a score would be updated each time a problem was attempted. In some cases, this seemed to harsh, since prior good work was “erased” easily. In some cases, this seemed to lenient, because sometimes an easy problem would earn a high score, but replace more thoughtful work on a harder problem. This semester scores were defined as the average of the scores from the last two attempts. This also made picking problems for re-assessments easier on me since I wasn’t as concerned about having them all be exactly the same difficulty. It also means that a score of 4 means a student demonstrated a strong level of mastery on two problems of a particular type, and that seems to work well.
  • I limited the number of re-assessments to one re-assessment topic per week. For example, if a student were struggling with Taylor Polynomials, they could come in throughout the week and try re-assessments. In some cases, they would just solve one problem. In other cases, they might solve four or five problems, each time getting a little more of the correct solution. Previously I let them do 2 standards per week but I found two problems with this: First, some students would just always pick their lowest two scores and try them, without really ever focusing on a single idea and working toward mastering it. Second, having multiple re-assessments on multiple topics times multiple students meant my grading workload was higher. So, one per weeks seems like a more manageable number for them to work on and it makes my grading workload lighter. Lastly, since we had 30 standards (but only 16 weeks) this policy pushed them to demonstrate mastery on in-class assignments (quizzes, exams) without just punting them to re-assess in my office later on.

Two things I don’t have data on yet:

  1. This semester I tried assigning online homework, with the homework contributing 5% to the overall course grade. I found assigning just textbook problems (and not grading them) did not work well. Perhaps I was not very good at motivating students to solve more problems on their own? I haven’t taken a detailed look at homework scores compared with course standing, so I am not sure if homework correlated with success on in-class assignments or not. I also feel a bit “icky” about assigning and grading homework, given some of the research I’ve seen.
  2. The other change I made was I separated “during semester scores” from “final exam scores.” So 70% of course grades will come from a letter grade assigned based on the scores on standards that were accumulated during the semester and 25% of course grades will come from a letter grade assigned based on scores on standards that will be accumulated on the final exam. This breakdown was in response to some conversations with students from last semester who felt that the old policy (“average of semester score and final exam score”) was too strict. We will see how this works out and if there is much movement in pre-final letter grades to post-final letter grades.

I’m teaching calculus II again in Spring 2015 and I plan to continue using this system. I am still entirely undecided about trying it in Pre-Calculus. I have several worries about trying it in that course.

Postscript: Here are some links to some older blog posts about my SBG Calculus adventure:

https://blogs.charleston.edu/owensks/2014/10/09/big-questions/

https://blogs.charleston.edu/owensks/2014/08/18/list-reboot/

https://blogs.charleston.edu/owensks/2014/02/25/on-the-purpose-of-examinations/

https://blogs.charleston.edu/owensks/2014/01/09/sbg-faq/

My Feedback Experiment

Posted on by
3

I’m trying something new in my exam grading process. I’ve been wondering for a while what sorts of comments to write on student solutions(1). My goals:

  • Convey to student what level of mastery their solution has demonstrated about the assorted topics
  • Convey to the student where any mistakes or errors were made
  • Avoid spending hours upon hours grading exams and/or leaving lengthy comments
  • Show positive & supportive sentiment

Recently, I’ve been writing questions instead of comments on exams. Some examples:

  • Rather than writing, “You forgot to use the quotient rule here” I’ll write instead, “How do we differentiate a quotient?”
  • Rather than correcting an antiderivative miscalculation, I’ll write instead, “Is the derivative of your answer equivalent to the integrand?”
  • Rather than fixing an arithmetical error, I’ll write instead, “Are you sure this should be 81?”
  • Rather than writing, “Your formula is wrong,” I’ll write instead, “What happens if we plug in x=4 on both sides?”

What I Wonder: I don’t know if what I’m trying is a good idea, a bad idea, or just totally crazy. When grading exams, I wonder (1) how to communicate mathematical corrections to a student and (2) how to be supportive of the emotions surrounding test-taking. I had a number of conversations this week with mathematicians about times they had really miserable experiences with feedback they got from their own math professors “back in the day.”

[It’s also interesting to me that we all seem to have stories of the form “The time my math professor made me cry was…”]

I really do not want to make any of my students cry about a calculus exam. I really do want to say helpful, supportive, thought-creating comments that help them move forward mathematically. I am trying to figure out how to balance both of these things. How do I say, “Your solution is wrong, but I really believe in you & your ability to mastery this material! Keep trying!”

Footnote (1): I’m completely ignoring what I know about the feedback & learning cycle. In particular, I am taking huge latitude here and ignoring the fact I know the research says I should be doing more formative assessment and less summative assessment. I’m also ignoring that I’m probably not going to be successful at my current quest because research has shown that regardless of what comments we give students, if we give them a grade at the same time, they tend to ignore the comments anyway. In fact, I’m going to ignore this so loudly, I won’t even track down the links to the ed journal articles I’ve read about this very thing.

Postscript. I went and hunted down some links to stuff I know about feedback. It all started when I asked something on Twitter:

Some stuff I learned:

and also, http://blog.mathed.net/2011/08/rysk-butlers-effects-on-intrinsic.html has a summary of Butler’s Effects on Intrinsic Motivation and Performance (1986) and Task-Involving and Ego-Involving Properties of Evaluation (1987).

Escaping the Lectureculture

Posted on by
1

For years now I’ve been a reader of Robert Talbert‘s column Casting Out Nines hosted by The Chronicle of Higher Education. Last week he wrote a post (“Is lecture really the thing that needs fixing?“) that gave me a lot to chew on. Here’s where I find myself today:

  1. Lectureculture is a set of machinery that self-replicates and it has political, social, psychological, instructional, and institutional components. It is pervasive and I find it in the world all around me, and some of the cultural natives don’t even recognize its existence.
  2. When I run a course, my #1 goal is to help learners move from being introduced to a concept to understanding and displaying mastery of the concept. Lecture is not the most effective way to help learners*.
  3. If I do nothing but lecture in my classes, I am helping sustain lectureculture and I am not helping my learners toward mastery the best I can, in violation of my #1 goal.

My plan of action: I’m teaching “Calculus II” again this semester. Although I’m using a standards-based approach, I must fess up that last semester nearly all of our class time was devoted to either lecture or assessment.

I am a lectureculture native and it is hard for me to let go. But I have come up with two ways I want to add non-lecture content delivery this semester (that don’t involve me tossing out all of my old materials).

First, I plan to continue last semester’s “Madness Mondays.” On those days, I introduced my students to ideas not necessarily tied to our course. I wanted to pick topics that I thought would inspire curiosity or happy befuddlement in my students, so they would walk away wanting to know more about what they had heard. (Examples: The Cantor set. Hilbert’s Hotel. Countably infinite vs uncountably infinite). I hoped to approach these ideas using a type of moderated discussion, letting the students ask questions to each other and talk about what was perplexing, interesting, fascinating, confusing, etc.

Second, I was really inspired by a recent video by Jo Boaler about “Number Talks” and I plan to try doing a weekly “Number Talk” (or something like it) with my calculus students.

My husband asked me why I wasn’t combining these things under one umbrella. To me, they hit two different–but equally important–goals for my course that can’t be found directly on our syllabus. They are

  1. I want my students to develop an appreciation for mathematics outside of what will show up on their next exam. I want them to be exposed to the kinds of questions mathematicians ask. I want them to practice the difficult skill of speaking with others about mathematical ideas.
  2. I want my students to become more fluent in numeration. I want my students to practice looking at the same problem from multiple perspectives. I want my students to see mathematics as a creative endeavor and get away from the idea that what mathematicians do is “apply a standard algorithm, proceed the same way, get the right answer.”

[Many of my digital colleagues seem to use some type of presentation requirement in their courses to get at item (1.) above. While I think that having students present math problems, solutions, ideas, etc. to each other would help develop this skill, and other skills too, I remember how terrified I was as an undergraduate at the thought of standing up in front of people and I don’t think I could impose those feelings on anyone in my classroom.]

Hopefully I will come up with other ways to push back against lectureculture in my classroom.

Footnote:
*As I was writing this post, the following MOOC announcement appeared in my Twitter feed & seemed quite apropos: